

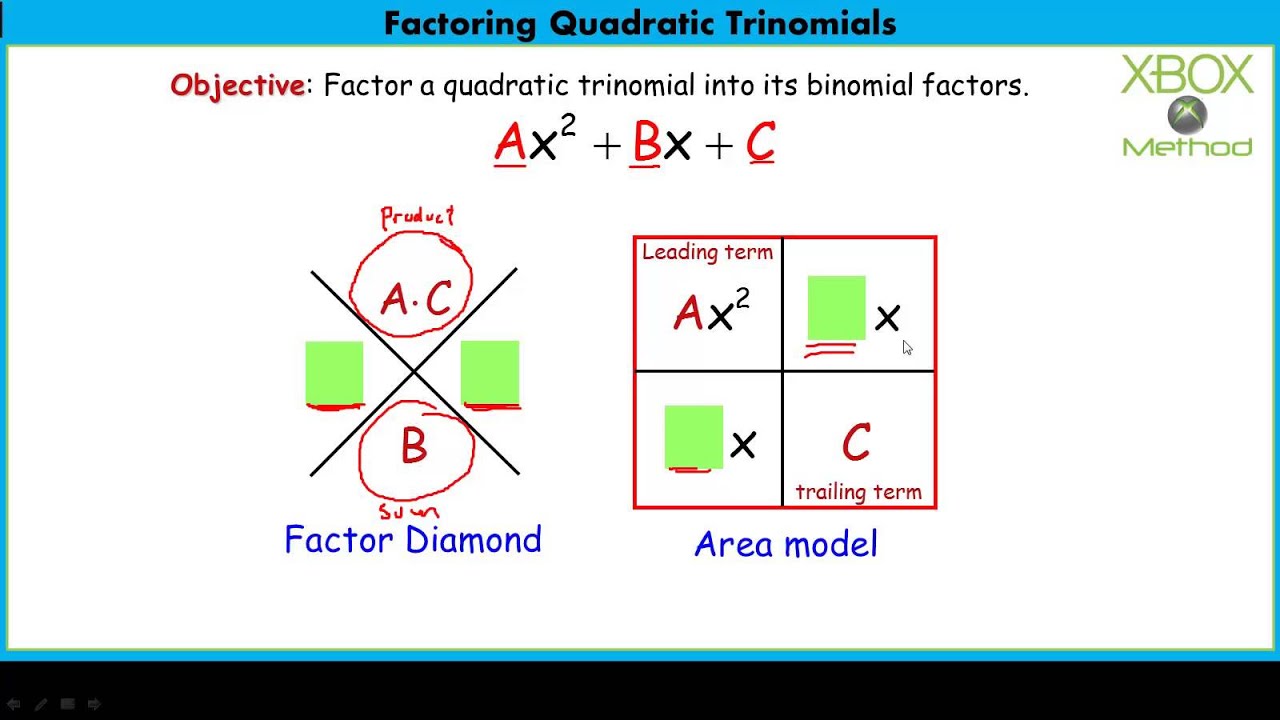
This gives:Īnd so we've successfully factored our trinomial.Īs you can see, it is only Step 1 that can pose some problems. We factor out (x + r/a) from the two summands we have. We factor out ax from ax² + rx and s from sx + r*s/a. We rewrite bx as rx + sx, and c as r * s / a, and so our trinomial takes the form: That is, we need two integers, r and s, such that: We need to determine two integers whose product is equal to ac and whose sum is equal to b. However, it may happen that a, b, c do not have a common factor and so we have to face the challenge of factoring the trinomial The remaining trinomial will have the leading coefficient equal to 1, so we arrive at the particular case discussed above. We are now ready to face the general case of factoring ax² + bx + c with any non-zero a.įirst of all, be aware that sometimes we can factor out a from all three terms. We factor out (x + r) from the two summands we have. We factor out x from x² + rx and s from sx + r*s. We rewrite bx as rx + sx and c as r * s, and so our trinomial takes the form: To correctly rewrite bx means to find two integers whose product is equal to c and whose sum is equal to b. That is, our trinomial is of the form x² + bx + c. We will start with the special case of quadratic trinomials with the leading coefficient a equal to 1.
First, however, let's summarize the procedure we've used above.
QUADRATIC TRINOMIAL HOW TO
We will teach you how to come up with the right way of rewriting the middle term bx of a quadratic trinomial so that you can easily finish the factorization. So, was it luck 🍀? Or magic 🧙🏻? Stay calm - it was mathematics. You should test similar transformations, likeĪnd see that they don't work. It is far from obvious why we've chosen such a transformation. That's it! We've written our trinomial as a product of two binomials.Īs you can see, the key step was to rewrite 8x as 2x + 6x. Let us first see an example of factoring trinomials by grouping to see how it works.įrom x² + 2x we can factor out x, and from 6x + 12 we can factor out 6:įrom the two summands we can factor out (x + 2):


 0 kommentar(er)
0 kommentar(er)
